Average Values (Average Particle Size)
There are various ways of considering the average value of particle size distribution (i.e. average particle size). On the SALD Series of laser diffraction particle size analyzers, since both graphs and tables displayed in data sheets are based on the logarithmic scale, the average value also is calculated based on not the normal scale but the logarithmic scale. However, note that the basic approach is the same as that for general average values excluding the point that the average value calculation is based on the logarithmic scale.
For example, the average value for the age of the Japanese (i.e. average age) and the average value for their weight are calculated according to the same approach. To calculate the average value for the age of the Japanese, all Japanese are broken down into categories by age, the numerical value for each age is multiplied by the number of people in each age group, and the sum is divided by the total population. The same method applies to particle size distribution, too. The value of each particle size should be multiplied by the normalized particle amount (difference %) and the result should be divided by the total normalized particle amount (100%).
Though the numerical values for age are discontinuous values with an increment of 1, the particle size values corresponding to these are continuous values in the case of particle size distribution. So, to calculate the particle size distribution, the distribution is divided into smaller intervals, a representative particle size is determined for each interval, and then representative particle sizes are substituted with discontinuous numerical values. Furthermore, since particle size intervals are based on the logarithmic scale, first the average value on the logarithmic scale is obtained, and the result is converted to an average value of particle size on a normal scale.
To be more exact, the particle size range (max. particle size: x1, min. particle size: xn+1) to be measured is divided into n separate intervals, and each of these particle size intervals is taken to be [x i , xi+1] (j = 1,2,.... n). The intervals in this case are equal divisions on the logarithmic scale. And, the representative particle size at each, individual particle size interval can be calculated as follows based on the logarithmic scale:
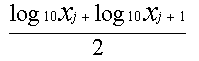
Since representative particle sizes are logarithmic values, they are no longer particle size values on a normal scale at this stage. Furthermore, let's take q j (j = 1,2,... n) to be the normalized particle amount (difference %) corresponding to each of particle size intervals [x i ,xi+1] and the total of all intervals to be 100%. Average value µ on the logarithmic scale can be calculated as:
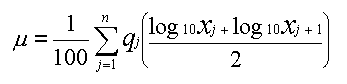
Since the µ is a numerical value on a logarithmic scale, 10µ, (10 to the power of µ) is calculated to obtain a particle size value on a normal scale.
On the SALD series, the value of 10µ is indicated on the data sheet as the average value (average particle size).


