Microparticle Packing Material
In recent years, ultra fast liquid chromatograph systems that use columns packed with microparticles as small as 2 µm have become popular. Using microparticles for packing materials allows improved and faster separation. This page discusses what it means to use microparticle packing materials, primarily in terms of the van Deemter equation.
Effective Height Equivalent to a Theoretical Plate (H) and the Van Deemter Equation
The number of theoretical plates (N) is an index widely used to indicate the level of peak separation. The larger the N value, the sharper the peaks, which is thought to enable higher separation. However, the N value also increases in proportion to the column length (L). Therefore, it does not indicate the separation efficiency (performance) of packing materials. Consequently, it has become popular to express the separation efficiency of a packing material independently of column length, in terms of the height equivalent to a theoretical plate (H), which is calculated as the column length (L) divided by the number of theoretical plates (N). In other words, it is the column length per theoretical plate.
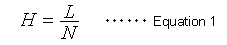
Equation 1 indicates that a smaller H value, a smaller L value or larger N value, means a more efficient packing material. A widely-known van Deemter equation (2) also expresses the relationship between the height equivalent to a theoretical plate (H) and column packing particle diameter and mobile phase linear velocity.
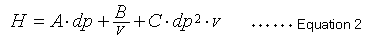
In this case, dp is the packing material particle diameter and v is the mobile phase linear velocity. This van Deemter equation comprises three independent terms that contribute to height equivalent to a theoretical plate (H). The first term in equation 2 (term A) is related to the diffusion of packing material particles through multiple flow lines and is proportional to the diameter of the packing particles. The second term (term B) is related to molecular diffusion and is inversely proportional to the linear velocity of the mobile phase. The third term (term C) is related to substance transfer and is proportional to the square of the particle diameter and the mobile phase linear velocity. Equation 2 indicates that decreasing the particle size also decreases terms A and C, which reduces the size of H.
Reducing the Packing Material Particle Size in Terms of the Van Deemter Curve
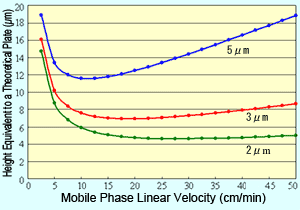
Fig. 1 Van Deemter Curves for Respective Packing Material Particle Sizes
Plotting the van Deemter equation results in curves like those shown in Figure 1. It shows how reducing particle size of the packing material reduces the height equivalent to a theoretical plate (H), which means a more efficient packing material. Also, it shows that when the packing material particle size is reduced, the linear velocity with the minimum H value is higher and the optimal linear velocity increases.
This means that reducing the packing material particle size allows using a shorter column and faster mobile phase flowrates without sacrificing separation. In other words, it enables performing analyses faster.
Advantages and Disadvantages of Microparticle Packing Materials
Theoretically, the van Deemter equation also means that reducing the particle size of the packing material enhances the column efficiency and optimal mobile phase linear velocity, allowing faster analysis. However, though microparticle packing materials provide such advantages, they also have the disadvantage of increasing pressure losses in the column.
Pressure losses in the column are described by equation 3 and are proportional to factors such as the mobile phase viscosity coefficient (ρ) for viscosity, column length (L), and the mobile phase linear velocity (v), and is inversely proportional to the square of the particle diameter (dp).
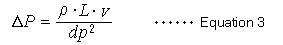
Based on this background, particle diameters have now been reduced to about 2 µm, to reduce the analysis time by several fold while providing separation equivalent to a typical HPLC system, which uses packing material with a particle size of about 5 µm.
Even though the pressure resistance of instruments have increased, there is a limit to how high it can be increased and pressure also affects the service life of consumables. Therefore, packing material particle size must be optimized to take advantage of the benefits of increased speed and higher separation, while mitigating its disadvantage of pressure. (Ma)


