Color measurement
1 Color
When a person views an object, light from a light source that is reflected from the object (or passes through the object) enters the eye and is collected by several types of photoreceptor cells in the retina. The proportion of light collected by these cells is sent to the brain and sensed as color. In practice, the simple proportion of light collected undergoes various processing as it passes along the nerves before being recognized by the person as color. Color measurements are a method of expressing the colors sensed by humans as values. Color measurements are related to illumination, spectral characteristics of the object, and the spectral sensitivity characteristics of the human eye. As the spectral distribution of the illumination and the spectral sensitivity characteristics (color-matching function) of the eye are defined in the JIS standards, a color value can be calculated if the spectral reflection of the object is known. (If the light passes through the object, the spectral transmittance can be used for the calculation. However, the spectral reflectance is used in the explanations below.) To explain in more detail, in the JIS standard, the spectral distribution of the illumination and colormatching function are calculated using multiple conditions. We are familiar with a change in color when the illumination is changed. Therefore, a different coefficient is set for each illumination spectral distribution. In addition, the color also changes according to the viewfield (viewing angle), due to the relationship with the sensitivity distribution characteristics of the retina. Consequently, the JIS standard sets different colormatching functions according to the viewfield. Color measurements require a wavelength range from 380 nm to 780 nm, which is equivalent to the wavelengths that can be sensed by the human eye. Color measurements can be made by calculations based on spectral reflectance measurements by a UV-VIS spectrophotometer across this wavelength range. Color measurement software is available for simple color measurements.
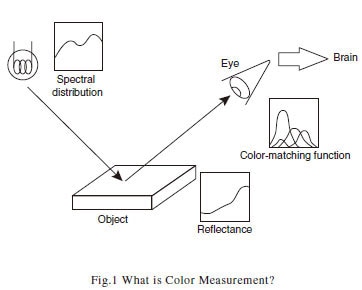
2 Color Measurement
To perform color measurements with a UV-VIS spectrophotometer, first measure the spectral reflectance of the object. Calculations based on the spectral distribution of the illumination, the spectral reflectance obtained for the object, and the color-matching function express the color as a numeric value. Illumination spectral distributions and colormatching function values are stored in the color measurement software to obtain color measurement values when the spectral reflectance spectrum is measured. The XYZ tristimulus values are the basis of color measurement. JIS Z 8722 "Methods of color measurement -- Reflecting and transmitting objects" calculates the XYZ tristimulus values using the expressions below.

Where,
S(λ): illumination spectral distribution value at wavelength λ
x(λ), y(λ),z(λ): color-matching function values in the XYZ color system
R(λ): sample spectral reflectance
Δλ: wavelength interval for calculation
In addition to the XYZ tristimulus values, several other color specification systems for expressing colors are known. The color measurement software can perform calculations in the following color specification systems: XYZ tristimulus values, xy color coordinates, Hunter Lab color scale, L*a*b* color system, L*u*v* color system, and U*V*W* color system. Values for color specification systems other than the XYZ tristimulus value system are calculated from the XYZ tristimulus values.
3. Color Difference
A color specification system is a method of expressing colors as numerical values, while color difference expresses the difference between colors. Calculations to numerically express color difference values use the Uniform Color Space (UCS) color specification system that is closer to the human visual sense. The L*a*b* color system is a typical UCS color specification system. L* represents the brightness, and a* and b* represent the hue and saturation. JIS Z 8729 "Colour specification -- CIELAB and CIELUV color spaces" shows the method of calculation in the L*a*b* color system. The color difference is calculated using the L*a*b* value for each object (sample) color. The color difference ΔE*ab in the L*a*b* color system is determined using expression (2) in JIS Z 8730 "Color specification -- Color differences of object colors."
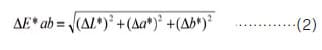
If the color coordinates of two objects (samples) are denoted L*1a*1b*1 and L*2a*2b*2, it can be seen from the expressions

that the color difference is equivalent to the distance between two points in the L*a*b* color space. The greater the difference between the two colors, the larger the color difference value. In addition to displaying the color system and the color difference in the color specification system, the color measurement software can perform other calculations including whiteness index, yellowness, major wavelengths, and excitation purity.
4 Setting Color Measurement Conditions
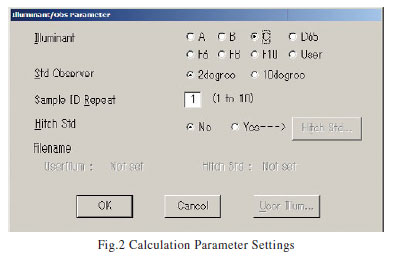
Several conditions are set for the color measurement calculations. These conditions are the illumination (light source) and viewfield (viewing angle). Settings for the illumination are required, as the color varies according to the illumination on the sample. Illumination settings include A, B, C, and D65. In the JIS standards, these are called standard illuminant and supplementary standard illuminant. The spectral distribution is different for each illumination. For example, standard illuminant A is used to calculate object colors under illumination by an incandescent light bulb. Standard illuminant D65 is used to calculate object colors in daylight including the UV light region. The color measurement software allows user-defined illumination settings to handle illumination conditions not provided as standard.
The viewfield (viewing angle) must also be set, as the color appears different when a sample is observed close-up or from a distance. For a viewfield up to 4 degrees, a 2° mean viewing angle is used for the calculations (color viewed from a distance); for a viewfield over 4 degrees, a 10° mean viewing angle is used for the calculations (color viewed close-up). The color-matching functions differ for a 2° mean viewing angle and a 10° mean viewing angle.
If the parameter settings are changed while reading the spectrum, the displayed color measurement values in the list change immediately. Fig. 2 shows the calculation parameter setting screen.
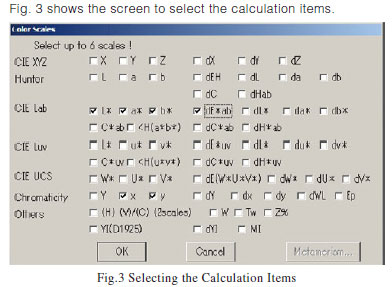
The color measurement software can simultaneously display up to six calculation items. If the calculation items are changed while reading the spectrum, the displayed color measurement values change immediately. Fig. 3 shows the screen to select the calculation items.
5 Spectral Reflectance Measurements
The measurement parameters must be set before measuring the spectral reflectance. To set the measurement parameters, set the photometric value (transmittance / reflectance), wavelength range (normally set from 380 nm to 780 nm), scan rate, slit width, and sampling pitch. Fig. 4 shows the measurement parameter setting screen.
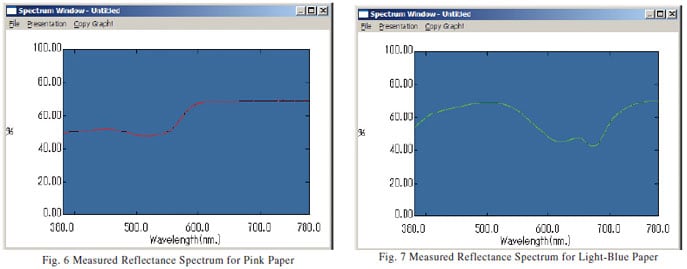
An integrating sphere is often used to measure the spectral reflectance of an object. Fig. 5 shows the photograph of an integrating sphere with a sample in position. The spectral reflectance can be measured by installing the sample as shown in the photograph. Fig. 6 and Fig. 7 show examples of spectral reflectance measurements using an integrating sphere. Fig. 6 shows the spectral reflectance measurement results for pink paper, and Fig. 7 shows the spectral reflectance measurement results for light-blue paper. Barium sulfate was used as the standard white plate for reference. The visible range encompasses the blue color system (400 nm to 500 nm), green color system (500 nm to 600 nm), and red color system (600 nm to 700 nm). The graphs show that the pink paper reflects more in the red color system, while the light-blue paper reflects more in the blue color system.
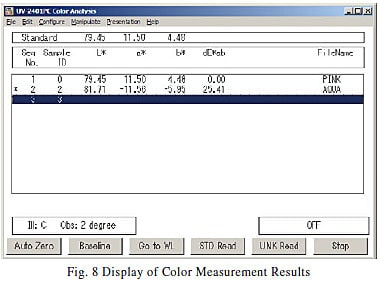
The color measurement values calculated from the spectral reflectance are displayed as a list. Naturally, calculations can also be performed on existing spectral reflectance data. Fig. 8 shows a display of the color measurement results. The calculation conditions were illumination C and 2-degree viewfield. The first row shows the color measurement results for the pink paper (L*=79.45, a*=11.50, b*=4.48 [red frame in diagram]). The second row shows the color measurement results for the light-blue paper (L*= 81.71, a*=-11.56, b*=-5.95 [blue frame in diagram]). The color measurement software can also display the color difference. The color difference is calculated based on a reference sample (the sample with ID set to 0 [green frame in diagram]). In this case, the pink paper is set as the reference sample. The color difference between the pink paper and the light-blue paper is ΔE*ab = 25.41 [black frame in diagram].
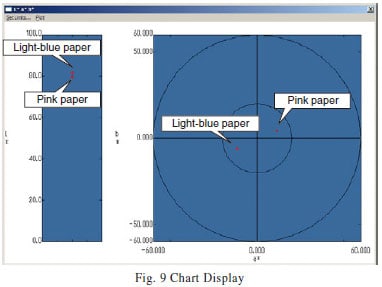
A chart display function shows the color measurement results in a clearly visible form. The color measurement results shown in the list display can be displayed as a chart. Fig. 9 shows the chart display of the color measurement results in Fig. 8. In the L* graph at the left, the color becomes brighter as the data point moves upward, and the color becomes darker as the data point moves downward. In the a*b* graph at the right, the color becomes duller as the data point moves toward the center, and the color becomes more brilliant as the data point moves toward the perimeter. In addition, the radius vector angle from the center represents the hue. For example, the top-right direction from the center of the circle represents red colors.
6 Data Correction
A standard white plate is used for the spectral reflectance measurements required to measure the object reflection color (color measurement by reflection). The standard white plates used include barium sulfate, magnesium oxide, alumina, and fluororesin. However, as these have high reflectance across the overall measurement wavelength range, adequate color comparison is possible if the same instrument is used. However, as a standard reflectance plate does not form a perfect diffusing surface and does not offer 100% reflectance, the spectral reflectance values measured for samples are relative values. Extremely high-accuracy measurements are required to make a comparison of the measured results obtained by different instruments. Making highly accurate measurements requires correction of the spectral reflectance to the spectral ratio reflectance with respect to a perfect reflection diffusing surface. The white plate correction function is used for this correction. By entering the spectral reflectance for the corrected standard white plate, the measured spectral reflectance is corrected to be equivalent to the measured results for a perfect reflection diffusing surface. Conversely, correction for the thickness is applied to measurements of the transmission color of an object (color measurement by transmission). A change in sample thickness results in a change in spectral transmittance that results in different color measurement results. Thickness correction is a function to determine the transmission color for the required thickness (target thickness).
Thickness correction by entering the actual measured thickness, the target thickness for which the color is to be determined, and the surface reflectance (or surface reflectance calculated from the refractive index) permits comparison of transmission colors between samples of different thickness. Thickness correction makes the following calculations. (See Fig. 10.)

- Determine the internal transmittance, excluding the measured surface reflectance of the sample.
- Apply thickness correction to the internal transmittance and subsequently add the surface reflectance.
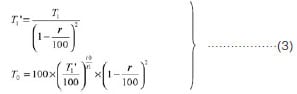
Expression (3) is used for actual thickness correction calculations to determine the transmittance T0 at each wavelength.
Where,
T1: measured transmittance (%)
T1': internal transmittance (%) with respect to measured
transmittance (%)
r: sample surface reflectance
t1: measured sample thickness [measured thickness] (mm)
t0: sample thickness to determine the transmittance for
[target thickness] (mm)
T0: calculated transmittance (%)
Instead of entering the surface reflectance, the value
calculated from the refractive index n using following
expression can be entered:
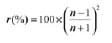
This yields 4% surface reflectance for glass with refractive index 1.5.Color calculations are performed after determining thicknesscorrected transmittance values at each wavelength.
7 Summary
JIS standards define calculation methods and coefficients for color measurements in detail. If the spectral reflectance is known, the calculations can be performed using spreadsheet software. However, different coefficients are required for different illumination and viewfields, which requires a huge number of inputs. The color measurement software can be used to select the conditions and measure the spectral reflectance to simplify color measurements.


