User Interview: Development of spectrometer for High-order Harmonic Generation (HHG)
Contents
2-1. Grating Resolution
If there are two spectrum lines corresponding to two neighboring wavelengths λ and λ+Δλ, the resolution is a measure of the extent to which Δλ can be reduced while still being able to distinguish between the lines. In general, the grating's diffracted light has a limited width defined by the diffraction limit. According to the "Rayleigh criterion", it is defined to be the limit for which resolution is possible when the first diffraction minimum for wavelength λ coincides with a maximum for wavelength λ+Δλ as shown in Fig. 2. In this case, the resolution λ/Δλ for a grating width of W is given by the following:
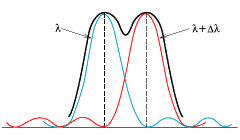
Fig. 2 Grating Resolution

Here, N × W is the total number of grooves in the grating. When the grating is actually used together with other optical elements (e.g., when incorporated in a spectrometer), however, aberrations and imperfections in other elements (e.g., lenses and mirrors) and factors related to the light source or the size of the slits may result in even wider spectral lines. This means that the minimum wavelength difference Δλ that can be resolved will be larger, and, in general, the resolution for the optical system will be lower than that for the gratings only defined by equation (6).
2-2. Free Spectral Range
It can be seen from the grating equation (2)' that when light of wavelength λ enters a grating, it is diffracted in many different directions corresponding to different values of m. As m only takes integral values, the diffraction angle β will take discrete values. For this reason, as shown in Fig. 3, when light with a wide range of wavelengths is directed at a grating, neighboring orders of spectra may partially overlap.
The range for which there is no overlapping is called the grating's "free spectral range." If the following equation is satisfied, mth-order light with wavelengths in the range λ1 to λ2 can be used without overlapping:
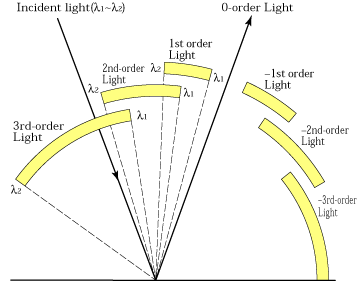
Fig. 3 Grating's Free Spectral Range
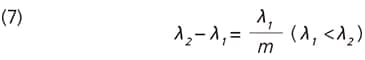
For example, when using first-order light with wavelengths greater than or equal to 350 nm, wavelengths up to 700 nm can be used without overlapping. The range 350 to 700 nm is the free spectral range. When using second-order light, the free spectral range is from 350 to 525 nm. As briefly described in the section on grating equations, however, it is necessary to use an appropriate groove density for light of wavelength λ2 at long-wavelength side, in this case 700 nm, to be obtained as diffracted one.
If the applied wavelength region is wider than the free spectral range, spectra corresponding to the unrequired orders must be removed from the overlapping region. For example, when using first-order light with wavelengths in the range 350 to 800 nm, a filter is used to cut the overlapping second-order light with wavelengths in the range 350 nm to 400 nm, in other words, to cut light with wavelengths of 400 nm or less. It is also possible to deal with overlapping by changing detectors.
2-3. Diffraction Efficiency
Diffraction Efficiency
The diffraction efficiency is a value that expresses the extent to which energy can be obtained from diffracted light with respect to the energy of the incident light.
In general, there are two ways of expressing the diffraction efficiency, "absolute diffraction efficiency" and "relative diffraction efficiency." The absolute diffraction efficiency is the ratio of the diffracted light intensity, of a given order, to the incident light intensity, and the relative diffraction efficiency is obtained by dividing the absolute diffraction efficiency by the reflectance of the coating material. Shimadzu adopts the relative diffraction efficiency. The values given in catalogs correspond to λB(Litt) for plane gratings and λB for concave gratings.
Relationship between Diffraction Efficiency and Polarization
Because the grooves in a grating are all etched in one direction, the diffraction efficiency can vary significantly with the polarization of incident light.
With S-polarization (TM waves), where the direction of the grating grooves and the oscillation direction of electric field vectors is perpendicular, large fluctuations in the diffraction efficiency can be observed.
Also, a high diffraction efficiency is exhibited for long-wavelength regions. With P-polarization (TE waves), where the direction of the grating grooves and the oscillation direction of electric field vectors is parallel, there is not as much fluctuation as with Spolarization, and the diffraction efficiency describe a smooth curve that peaks at the blaze wavelength.
Fig. 4 shows the results of calculating the diffraction efficiency in the Littrow configuration for different polarizations. The horizontal axis represents the ratio of the wavelength λ to the grating period d, i.e., λ/d.
For larger blaze angles (grooves depth for sinusoidal gratings), scalar theory becomes less applicable and the diffraction efficiency varies greatly with the polarization.
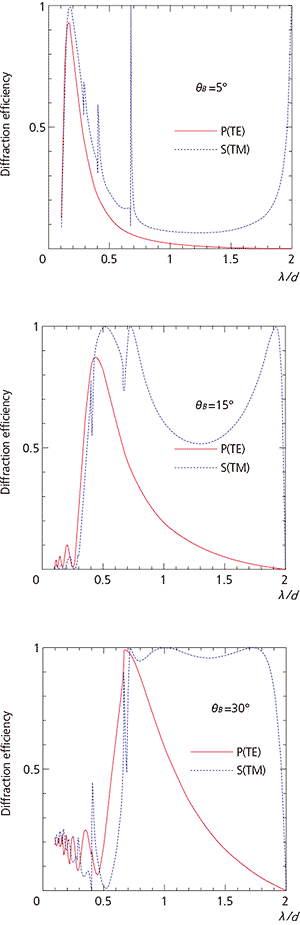
Fig. 4 Relationship between Diffraction Efficiency and Polarization
2-4. Anomalies
When using a diffraction grating to observe spectra, there are times when spectral intensity changes suddenly. Such phenomena are called "anomalies." They are particularly noticeable with S-polarization(TMwave).
These anomalies occur for diffracted light of order m'and wavelength λ that is diffracted at an angle of β = ±90° (passing-off conditions), and are called "Wood's anomalies."



