User Interview: Development of spectrometer for High-order Harmonic Generation (HHG)
Contents
4-1. Master Fabrication Process
A grating produced by a holographic exposure method that adopted the two beams interference of laser beam is called a "holographic grating" (HG). With holographic gratings, there is very little stray light due to periodic errors, and concave holographic gratings (concave HG) have the highly useful property of being able to correct aberrations within the grating itself. After many years of joint research together with the RIKEN Institute of Physical and Chemical Research, we succeeded in blazing a holographic grating, something that ion-beam etching technology. Based on this, we were the first to develop the technology for manufacturing blazed holographic gratings (BHG), which, compared to conventional mechanically ruled gratings, ensure less stray light without any reduction in diffraction efficiency. (See Fig. 7.) This unique grating manufacturing technology was patented in Japan as Japanese Patent No. 1046763 and was awarded the Okochi Memorial Prize. In order to facilitate more effective aberration correction for the wavelength region used in different types of gratings, Shimadzu developed an aspherical wave exposure method that uses aspherical waves for holographic exposure method. As a result, it is now possible to custom-design gratings of excellent performance to match the characteristics of different types of spectroscopic devices.
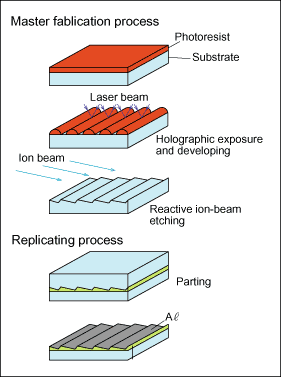
Fig.7 Fabrication Process
for Blazed Holographic Gratings
4-2. Replicating Process
Shimadzu gratings are made by replicating a master. The grating grooves are formed with resin on top of a glass substrate (blank), as shown in Fig. 8. A reflective coating (e.g., Aℓ) is applied to the grooves. Moreover, we have also the replica diffraction grating which have passed the tests in accordance with Telcordia GR-1221-CORE for optical communication. Because the grating grooves are formed with resin, care is required for use or storage in locations with high temperatures or high humidity conditions.
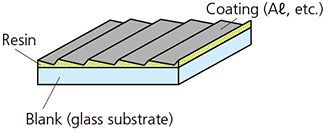
Fig. 8 Replica Grating
4-3. Coatings
The energy in the diffracted light varies with the grating's coating material. It is necessary to use the coating material that is appropriate for the required wavelength. Fig. 9 shows the reflectance characteristics for Aℓ , Aℓ+MgF2, and Au.
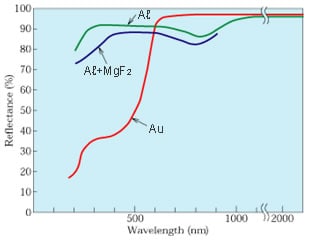
Fig. 9 Reflectance of Aℓ, Aℓ+MgF2, and Au



