3. Grating Grooves

3-1. Profile of Grating Grooves

Gratings can be classified into several different types according to the profile of the grooves. The respective features of three types of gratings manufactured by Shimadzu are described below

1 . Blazed Holographic Gratings (BHG)

Sawtooth Grooves

• These gratings exhibit a high diffraction efficiency for specific wavelengths in a range from ultraviolet to visible light.
• The blaze wavelength (the wavelength corresponding to peak diffraction efficiency) is determined by the blaze angle.
• They can be used in spectroscopes for ultraviolet and visible light.

2 . Holographic Gratings (HG)

Sinusoidal Grooves

• These gratings offer a relatively high diffraction efficiency at a broad range of wavelengths.
• The wavelength corresponding to the peak diffraction efficiency is determined by the groove depth.
• In general, the diffraction efficiency is around half that of blazed holographic gratings(BHG) but the values of groove depth / period are large, it may be possible to obtain an efficiency greater than that of BHG.
• They are used for wide wavelength regions and the near infrared range.

3 . Laminar Gratings

Rectangular Grooves

• The diffraction efficiency for even orders of light is lower than that of BHG and HG.
• The wavelength corresponding to the peak diffraction efficiency is determined by the groove depth.
• They are used in the soft X-ray region as a large reflectance can be attained in this region.

3-2. Blaze Wavelength

Gratings with grooves that have a sawtooth profile (blazed gratings) exhibit a high diffraction efficiency for certain orders and wavelengths.
In Fig. 5, light is directed at a reflective grating at angle α and light of wavelength λ is diffracted at angle β. Here, α and β are the angles made with the normal to the grating and counterclockwise direction is taken as positive. Grating equation (2)' can be updated as the following relationship:

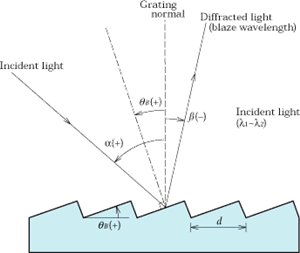
Fig.5 Reflective Grating

When the relationship between the incident light and the mth-order diffracted light describes mirror reflection with respect to the facet surface of the grooves, most of the energy is concentrated into the mth-order diffracted light. The facet angle of the grooves at this point is called the "blaze angle" and, represented by θ_B, satisfies the following:

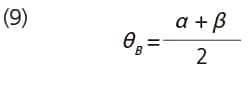
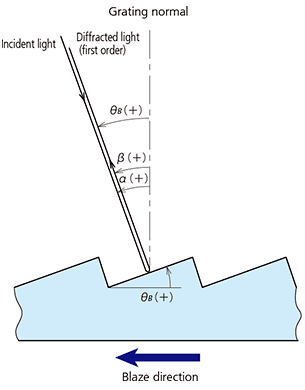
Fig. 6 Littrow Mounting

The corresponding wavelength is called the "blaze wavelength" and is represented by λ_B. Combining equations (8) and (9) gives the following:

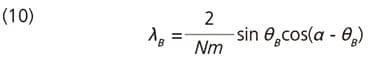
It can be seen from this equation that the blaze wavelength varies with the blaze angle θ_B and the incident angle α (i.e., the usage method). In gerneral, the wavelength (λ_B(Litt)) where first-order diffracted light returns along the same path as the incident light is used to represent the blaze characteristics of gratings. In this case, α = β = θ_B then equation (8) gives the following:

This is called the "Littrow mounting". In our catalogs, the blaze wavelengths given for plane gratings are the blaze wavelengths for this configuration. Equation (12) is Substituted equation (11) for equation (10) and applied m to both sides.

The relationship between the blaze wavelength λ_B for other configurations and the blaze wavelength λ_B(Litt)used in the catalog is given by the following:

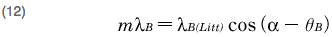
It can be seen from this equation that, when not using the Littrow configuration, the blaze wavelength λ_B is shorter than λ_B(Litt).
For incident angle α, the relationship between λ_B(Litt) and λ_B is given by the following:

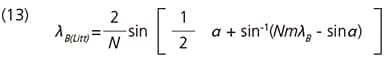
For example, for a groove density N of 600 grooves/mm and an incident angle α of 60°, in order to obtain first-order light with a wavelength of 300 nm, substiture λ_B = 300 nm in equation (13) to obtain λ_B(Litt) = 484 nm. In this case, then, select a grating for which λ_B(Litt) = 500 nm from the catalog.
The blaze wavelengths given for concave gratings in catalog are the blaze wavelengths for the configuration (mounting) in the optical system used.
The arrows on the gratings indicate the blaze direction and the relationship between the groove profile and this direction is shown in Fig. 6.

Line up

Diffraction Gratings